Steam turbines are a fundamental component in thermodynamics. They are used in a variety of different types of systems, aiding in both power and heat generation. In a steam turbine, water is the working fluid which passes through the system. Steam turbines work by allowing pressurized water vapor to expand through the turbine blades, causing them to rotate and generate power. Their individual purpose is to provide power. The simplest form of the steam turbine is isentropic. This simply means the system is ideal and has no loss of energy. This Instructable will teach you how to solve for the work generated in an isentropic steam turbine.

Step 1: Identifying Knowns and Unkowns

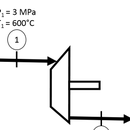
Before we get to identifying values, I will briefly explain the diagram. The trapezoid represents the turbine, and the rectangle coming out of the trapezoid represents the power generation component of the turbine. The arrows represent the flow of the water through the turbine. This is a fairly standard diagram method used throughout thermodynamics.

Determine the knowns and the unknowns of the given example. In the vast majority of problems involving a steam turbine, you will be required to solve for net work (Wdot). Create a state table identifying the before and after states (states one and two) where you will record this data. Record all of the following that are given: temperature, mass flow rate (mdot), and pressure.

Units use standard SI prefixes. Some of the units you may not be familiar with are:

Pascals (Pa) - a unit of pressure

Joules (J) - a unit of energy

Once you have filled in your state table with the given values, determine what system of units you are in, and find this section of the water tables in the appendix of the book.

Step 2: Finding Tables

Using either your thermodynamics textbook or a reputable database, we will now write down the needed properties.

These data tables contain thousands of values regarding energy content and other values for assorted fluids. They are used on a daily basis to analyze power systems.

All of our properties for this example and many others will be found in the superheated tables. For a steam turbine, the water entering the turbine (at state one) must be superheated in order to avoid mechanical failure. Typically, state two will also be superheated.

The picture above displays the needed tables for the example.

Step 3: Recording Properties

Once you have found the appropriate tables, you will now begin recording the necessary properties. For this example, we will only need specific enthalpy (h) and specific entropy (s).While you are in the superheated water tables, record the appropriate h and s values. For state one, this will simply be matching your temperature with one in the table. Finding state two properties is a bit more difficult. In order to find the h value for state two, we need to know the entropy of state two. For an isentropic turbine, s1=s2. Using this knowledge you can find your values for state 2. Find a value or range of values in the new pressure section that matches the entropy recorded from state one. This may require you to interpolate depending on the entropy value. Keep in mind: For a steam turbine, you will always be superheated in state 1 and typically state 2 as well.

The above picture contains the completed state table.

Step 4: The Equation

It is important to understand the fundamentals of the equation you will be using to solve. The equation we will be using is the simplified open system conservation of energy equation:

dE/dt represents the overall rate of change of energy in the system.

Q(dot) represents the rate of heat transfer in the system.

W(dot) represents the work transfer in the system.

m(dot) represents the mass flow rate of the working fluid (water) through the system.

For this problem and the vast majority of the steam turbine problems you will work, Q(dot) and dE/dt are equal to 0, since there is no net change in energy of the system and there is no heat lost or gained. Typically, you will be given a mass flow rate and will be asked to solve for net work. In a turbine, it is important to remember that the final term for work is positive, as the turbine’s purpose is to generate work.

Step 5: Evaluating the Equation

Before we begin solving, make sure to once again check units of given values and also units requested in the final answer. Note any needed conversion factors to reference during calculation.

Plug in all values into the equation and solve for the missing piece, be sure to include appropriate conversion factors.

Report answer in the requested units (if applicable).

Step 6: Checking Your Work

For this problem, the work generated by the turbine is approximately 2360 kW or 2.36MW. Check your work and if incorrect be sure to review properties and units.

You now know how to evaluate an isentropic steam turbine.