Using the Concept of a Folding Rule When Teaching Students About Polygons

In this Instructables we suggest that the concept of a folding rule may be useful when teaching students about polygons. This idea of using the concept of a folding rule for this Instructables developed after reading a problem in the Pre-Algebra Problem of the Week resources provided by the National Council of Teachers of Mathematics. This resource suggested that students use the concept of a folding rule to generate equilateral, isosceles and scalene triangles.

Most school students are familiar with regular polygons (polygons whose sides or edges have equal lengths and whose angles between adjacent sides are all equal), like those found in equilateral triangles and squares. Students are however less familiar with irregular or non-regular polygons other than those related to quadrilaterals, like rectangles and parallelograms.

Except for the first and last strips, most folding rules can be regarded as polygonal chains made up of n straight segments, or strips, of length equal to the length of strips of the folding rule. The length of the two end strips of a folding rule is shorter than the length of the remaining strips by a distance equal to the distance between the center of any one of the rivets or hinge pins linking the individual strips and the nearest edge of a strip (see above photo, which shows part of the left end of a 2 m folding rule with eight 24 cm internal strips and two 22 cm end strips and with hing pins 2 cm from the thin ends of the strips).

While there are many configurations that a polygonal chain can take up, we restrict the discussion in this Instructables to those polygonal chains made up of n straight segments of equal length having a fixed angle (denoted by α) between all adjacent segments. The polygons discussed here are those obtained by drawing a straight line between the two unattached ends of the segments at the ends of the polygonal chain. (All segments of a polygonal chain are attached to two other adjacent segments except for the first and last segments of the chain.).

Fixing the angle between all adjacent segments of a polygonal chain and drawing a straight line between the two ends of the two end segments of the polygonal chain will, except for cases where:

the distance between the two ends of the two unattached end segments of the polygonal chain equals the length of the polygonal chains' segments, or where:
the two ends of the two unattached end segments of the polygonal chain touch each other,

result in a class of polygons that have the following two properties:

except for one edge, all edges are of equal length;
except for two equal adjacent angles, all other adjacent angles are equal.

Some of these polygons will be simple polygons whose edges never cross, while others will result in self-intersecting polygons where one of the edges crosses one or more of the other edges, like those found in star polygons.

In what follows, in Step 1 we provide a brief introduction to Schläfli notation for describing regular polygons and regular star polygons, and in Steps 2 to 6 we see if any patterns begin to emerge after examining polygonal chains with 2, 3, 4, 5 and 6 segments as the angle α is reduced from 180° to 0°. All diagrams in Steps 2 to 6 were drawn using a ruler and protractor.

Step 1: Brief Introduction to Schläfli Notation and Regular Star Polygons

For the polygons described in this Instructables we use Schläfli symbols as a notation to describe regular polygons. For simple regular polygons having n vertices and sides, the polygon is described by enclosing the letter n in curly brackets: {n}. The notation for regular star polygons requires two letters, which will become obvious when we describe one of the procedures that can be followed for drawing such star polygons.

Consider a regular pentagon as shown in the left-hand corner of the top row in the above diagram. If we draw lines between each vertex and the second vertex further along from each vertex as shown in the middle image in the top row of the above diagram, we obtain (after removing the outline of the simple regular pentagon) a regular star polygon as shown in right-hand corner of the top row in the above diagram.This regular star polygon is known as a pentagram (all its internal angles are 36°) and its Schläfli symbol is {5/2}, where the first number denotes the number of vertices or sides of the regular star polygon and the second number is the number of vertices skipped plus 1 in the simple regular polygon when drawing each edge of the star.

If we repeat this procedure for a heptagon and also repeat the procedure by drawing lines between each vertex and the third vertex further along from each vertex, we find that there are two possible regular star polygons (heptagrams): the one on the left side of the second row in the above diagram is denoted by {7/2} (all its internal angles are 77¹/₇° ≈ 77.143°) and the one in the middle of the same row is denoted by {7/3} (all its internal angles are 25⁵/₇° ≈ 25.714°). (Internal angles are the angles between adjacent sides of regular polygons and are given above as they will be mentioned again in Steps 4 to 6.)

When we draw lines between each vertex and the second vertex further along from each vertex for a hexagon as shown in the left-hand image in the second row of the above diagram, we obtain a regular hexagram {6/2}. Removing the outline of the regular hexagon, we obtain the image shown in the lower left-hand corner of the lower row in the above diagram. However this hexagram is different from the other regular star polygons that we have just described. The earlier polygrams can be regarded as unicursal polygrams, which describes the fact that the polygram can be drawn without lifting the drawing instrument from the page, just like with cursive handwriting. The hexagram {6/2}, on the other hand, is made up of two equilateral triangles, and the total figure (the hexagram) cannot be drawn without lifting the drawing implement from the page. Such types of regular polygrams are known as regular compound polygons and are regarded as degenerate regular star polygons. They could therefore also be called non-cursive polygrams.

In the Wikipedia article discussing the interpretation of {6/2}, it is noted that the interpretation of /2 in the previous paragraph is that due to older school geometers and is regarded by many modern geometers as incorrect. To quote from the Wikipedia article, many modern geometers:

take the /2 to indicate moving two places around the {6} at each step, obtaining a "double-wound" triangle that has two vertices superimposed at each corner point and two edges along each line segment.

Such a doubly-wound hexagon is shown in the image in the lower right-hand corner of the lower row in the above diagram, where the numbers, 1, 2, 3, 4, 5 and 6 are the vertices of the hexagon arranged in sequential order.

In this Instructables we will refer to {6/2} as a doubly-wound hexagon. Similarly, we will refer to {8/2} as a doubly-wound octagon and {10/2} and {10/4} as a doubly-wound decagon and a doubly-wound decagram, respectively.

Step 2: Polygonal Chain Consisting of 2 Segments

We first consider the simplest polygonal chain, namely, one that is made up of two segments. As a real world example of such a polygonal chain, one can consider a foldable plastic 12 inch or 30 cm. school ruler that can easily be stored in a small pencil case (see above photo). We describe the foldable ruler as two straight lines AB and BC linked together at point B.

In this step and the following steps we describe the various stages taken up by the polygonal chain and the line joining its unattached ends as the angle α between all the attached segments is reduced from 180° to 0°. The various stages are indicated by consecutive numbers and bold letters are used to indicate whether the polygons formed are regular or irregular.

When the chain is fully extended, α = 180°, and we have a straight line of length equal to twice the length of each segment.
As α is reduced from 180°, at first, one of the simplest irregular polygons is formed, namely an obtuse isosceles triangle.
When α = 60°, the simplest regular polygon is formed, namely an acute equilateral triangle.
Further reduction of α below 60° results again in the formation of an irregular polygon, namely an isosceles triangle.
Eventually, when α = 0°, the sides AB and BC of this isosceles triangle will lie on top of each other with the unattached ends A and C of the segments AB and BC touching each other so that the distance between the unattached ends A and C is zero.

Step 3: Polygonal Chain Consisting of 3 Segments

The solid lines in the above diagram show a polygonal chain made up of three segments, AB, BC and CD at two stages when ∠ABC and ∠BCD take on a value that is obtuse (left image) and a value that is acute (right image). The dotted line is the line drawn between the unattached ends of the end segments AB and CD. As in the previous step, we now list the various stages taken up by the polygonal chain and the line joining its unattached ends as α is reduced from 180° to 0°.

When the chain is fully extended, α is 180° and we have a straight line of length equal to three times the length of each segment.
As α is reduced from 180°, the distance between the unattached ends of the end segments decreases and an irregular polygon is formed, namely an isosceles trapezium as shown in the figure on the left-hand side of the above diagram. The distance between the unattached ends of the end segments, AD, is less than three times the length of the individual segments.
When α = 90°, the distance between the unattached ends of the end segments equals the length of each of the individual segment and a regular polygon is formed, namely, a square {4}.
When α < 90°, the distance between the unattached ends of the end segments decreases even further, again resulting in the formation of an irregular polygon.
Eventually, when α = 60°, points A and D coincide, resulting in the formation of a regular polygon, namely an equilateral triangle {3}.
When α < 60° an irregular polygon is formed in which the first and last segments of the polygonal chain cross over each other as shown in the image on the right-hand side of the above diagram. This complex quadrilateral is known by a number of names, such as, a self-intersecting quadrilateral, a cross-quadrilateral, a crossed quadrilateral, a butterfly quadrilateral or a bow-tie quadrilateral. As α decreases from 60°, the length of AD increases and approaches a length equal to each of the individual segments.
Eventually, this 4-sided irregular quadrilateral becomes a straight line when α = 0° with all three segments lying on top of each other. Points A and C overlap each other, as do points B and D and the distance between the unattached ends of the end segments of the polygonal chain is equal to the length of an individual segment of the polygonal chain.

Step 4: Polygonal Chain Consisting of 4 Segments

The solid lines in the above diagram show a polygonal chain made up of four segments, AB, BC, CD and DE at a number of different values of α. The dotted line is the line drawn between the unattached ends of the end segments AB and DE. We now list the various stages taken up by the polygonal chain and the line joining its unattached ends as α is reduced from 180° to 0°.

When the α = 180°, the polygonal chain is fully extended, and we have a straight line of length equal to four times the length of each segment.
When 180° > α > 108°, an irregular 5-sided pentagon is formed, such as the one shown on the left-hand side in the top row of the above diagram. The length of the line drawn between the unattached ends of the four segments is less than four times the length of the length of each individual segment.
When α = 108°, the length of the line drawn between the unattached ends of the end segments, AE, equals the length of each of the individual segments and a regular polygon, namely, a regular pentagon {5} is formed.
When 108° > α > 90°, once again an irregular polygon as shown on the right-hand side in the top row of the above diagram is formed. As the angle decreases towards 90°, the line drawn between the unattached ends of the end segments decreases and approaches zero.
When α = 90°, the unattached ends of this polygonal chain, A and E, meet and a regular polygon, namely a square {4} is formed.
When 90° > α > 60° the end segments AB and DE cross over each other, with the the line drawn between the unattached ends of the end segments, AE, increasing as the angle between the segments approaches 60°. The line AE does not cross any of the other segments of the polygonal chain. Between 90° and 60° we have and irregular polygon that can be described as a self-intersecting irregular pentagon, an example of which is shown in the image in the lower left-hand corner of the above diagram..
When α = 60°, the self-intersecting irregular pentagon becomes a regular polygon, namely a doubly-wound hexagon {6/2} that is missing two of its overlapping sides when segment AB overlaps segment DE.
When 60° > α > 36°, again a self-intersecting irregular pentagon (an irregular star pentagon) is formed as shown in the middle image in the lower row of the above diagram. Note that each side overlaps two other sides:
AB overlaps CD and DE;
BC overlaps DE and EA;
CD overlaps EA and AB;
DE overlaps AB and BC;
EA overlaps BC and CD.
Furthermore, note that the distance between the unattached ends of the end segments (EA) increases as the angle is reduced from 90° and that it is greater than the the length of each individual segment (e.g., compare the lengths of EA and AB in the middle image in the lower row of the above diagram). Eventually, at some particular angle it reaches a maximum length before the angle reaches a value of 36° (see the following stage).
When α = 36°, the distance between the unattached ends of the first and last segments equals the length of the individual segments, and a regular star polygon known as a pentagram {5/2} is formed..
When α < 36°, an irregular star pentagon is again formed, an example of which is shown in the image in the lower right-hand corner of the above diagram. As α is further reduced below 36°, the length of the line drawn between the unattached ends (A and E) of the end segments decreases and approaches zero.
This 5-sided irregular star polygon formed in Stage 10 eventually becomes a straight line when the angle between the segments is 0° with all four of its segments lying on top of each other with the ends of the unattached segments touching each other. Points A, C and E overlap each other as do points B and D, so that the distance between the unattached ends of the end segments is equal to zero.

Step 5: Polygonal Chain Consisting of 5 Segments

The solid lines in the above diagram show a polygonal chain made up of five segments, AB, BC, CD, DE and EF at a number of different values of α. The dotted line is the line drawn between the unattached ends of the end segments AB and EF. We now list the various stages taken up by the polygonal chain and the line joining its unattached ends as α decreases from 180° to 0°.

When α = 180°, the chain is fully extended and its length is five times the length of the length of each individual segment.
When 180° > α >120°, an irregular 6-sided hexagon is formed, such as the one shown in the top left-hand corner in the above diagram. The length of the line drawn between the unattached ends of the five segments is less than five times the length of each individual segment.
The length of AF decreases until its length equals the length of each individual segment when α = 120°. When this angle is reached the figure becomes a regular hexagon {6}.
As α is further reduced from 120°, the length of AF is further reduced and an irregular hexagon is again formed.
Eventually the unattached ends of the polygonal chain touch each other (at 108°) when a regular pentagon {5} is formed.
As α is further reduced from 108° the first and last segments of the polygonal chain cross over each other resulting in an self-intersecting irregular hexagon as shown in the middle image in the top row of the above diagram.The length of the line drawn between the unattached ends of the polygonal chain, AF, increases as the angle approaches 90°. The line AF does not cross any other segments of the polygonal chain.
When α = 90° the first (AB) and last (EF) segments of the polygonal chain overlap and the resulting figure is a regular polygon, namely a doubly-wound octagon {8/2} that is missing three of its overlapping sides.
As α is further reduced from 90° we again have a self-intersecting irregular hexagon an example of which is shown in the top right-hand corner of the above diagram. Now an adjacent pair of end segments at one end of the polygonal chain cross over a corresponding adjacent pair of segments at the other end of the chain (segments AB and BC cross over segments DE and EF). The line drawn between the unattached ends of the five segments at first increases in length but then decreases as its length approaches the length of each of the individual segments.
When α = 60° the length of the line drawn between the unattached ends of the five segments equals the length of each of the individual segments resulting in the formation of a regular polygon, namely a doubly-wound hexagon {6/2} that is missing one of its overlapping sides when segments AB and BC overlap segments DE and EF.
As α is further reduced from 60°, the line drawn between the unattached ends of the polygonal chain decreases in length again forming an irregular self-intersecting hexagon, examples of which are shown in the left and middle images in the lower part of the above diagram. Under these conditions, all sides, except the line joining the unattached ends of the first and last segments of the polygonal chain (AF), cross over two other sides:
segment AB crosses over segments CD and DE;
segment BC crosses over segments DE and EF;
segment CD crosses over segments EF and AB;
segment DE crosses over segments AB and BC;
segment EF crosses over segments BC and CD;
The line joining the unattached ends of the first and last segments of the polygonal chain (AF) does not cross any of the other segments. Again the figure obtained is a self intersecting irregular hexagon as shown in the left corner and middle images of the lower row of the above diagram.
When α = 36° the unattached ends of the first and last segments of the polygonal chain touch each other resulting in a regular star pentagon, known as a pentagram {5/2}. This time, all sides of the polygonal chain which crossed over two other sides in the previous stage still cross over the same two other sides but the side joining A and F does not exist as the two points A and F coincide.
As the angle between the segments is further reduced, the unattached end segments cross over each other again (as we had after the formation of an irregular hexagon in Stage 6) resulting in the formation of an irregular self-intersecting hexagon an example of which is shown in the image in the lower right corner of the above diagram. This time the length of the distance between the ends of the unattached segments will increase until they equal the length of the individual segments.
At 0°, all five segments eventually overlap each other with points A, C, and E lying on top of each other and points B, D, and F also lying on top of each other, thus making the distance between the unattached ends of the end segments equal to the length of an individual segment of the polygonal chain. .

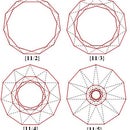
Step 6: Polygonal Chain Consisting of 6 Segments

Instead of describing all the details as done in the previous steps, we now list the various geometric figures that are obtained as α ranges between 180° and 0°.

When α = 180°, the chain is fully extended and its length is six times the length of each individual segment.
When 180° > α > 128⁴/₇°, an irregular 7-sided heptagon is formed.
When α = 128⁴/₇°, a regular heptagon {7} is formed.
When 128⁴/₇° > α < 120°, anirregular 7-sided heptagon is formed.
When α = 120°, a regular hexagon {6} is formed.
When 120° > α > 108°, an irregular self-intersecting heptagon is formed.
When α = 108°, a regular polygon is formed, namely a doubly-wound decagon {10/2} that is missing four of its overlapping sides.
When 108° >. α > 90°, an irregular self-intersectng heptagon is formed.
When α = 90°, a regular polygon, is formed, namely a doubly-wound octagon {8/2} that is missing two of its overlapping sides.
When 90° > α > 77¹/₇°, an irregular star heptagon is formed.
When α = 77¹/₇°, a regular star heptagram {7/2} is formed.
When 77¹/₇° > α > 60°, a irregular star heptagon is formed.
When α = 60° a regular polygon, namely a doubly-wound hexagon {6/2} is formed.
When 60° > α > 36°, an irregular self-intersecting heptagon is formed.
When α = 36° a regular polygon is formed, namely a doubly-wound decagram {10/4} that is missing four of its overlapping sides.
When 36° > α > 25⁵/₇°, an irregular self-intersecting heptagon is formed.
When α = 25⁵/₇°, a regular star heptagram {7/3} is formed
When 25⁵/₇° > α < 0°, an irregular self-intersecting heptagon is formed.
When α = 0°, all segments overlap each other and the distance between the unattached ends of the end segments is zero.

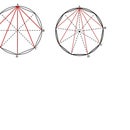
It is worth noting that in Stages 10 and 12, we refer to the irregular polygons as irregular star heptagons whereas in Stages 14, 16, and 18, we refer to the irregular polygons as irregular self-intersecting heptagons. The image on the left in the above diagram shows one of the images of the polygonal chain and the line joining the unattached ends of the end segments of the polygonal chain during Stage 10 while that on the right shows one of the similar images during Stage 16. The lines emanating from any pair of adjacent points A, B, C, D, E, F and G in the left hand image cross each other at a single point before crossing any other lines, whereas those emanating from points E and G, and from points A and C, in the right-hand image, cross lines BC and EF respectively before meeting at a point. In order to be considered a star polygon, all lines emanating from adjacent outside points of a star must not cross any other line before meeting at single point.

Conclusion

Based on observations made in Steps 2 to 6, we suggest that, as the angle α between equal length segments of a polygonal chain of n segments is reduced from 180°, the geometric figures formed are non-regular polygons with (n + 1) sides that alternate with unicursal regular polygons or regular star polygons whenever α takes a value which results in a figure being a unicursal regular polygon or a unicursal regular star polygon.