A Method for Finding the Lengths of All the Diagonals of a Regular Polygon

In the book The Perfect Sausage and other Fundamental Formulas (one of the books in the British series of educational books Murderous Maths), there is a problem and its solution for finding the length of the longest diagonal of a polygon with an odd number of sides. While the solution presented is straightforward, this Instructables presents another way to look at this problem, and also provides an answer for the lengths of all the different diagonals present in both odd- and even-sided polygons. In order to work out the lengths of all the diagonals, this Instructables extends the notation presented in an earlier Instructables, and expresses the lengths of all the diagonals of a regular polygon in terms of either the length of the side of the polygon or the radius of the circumscribed circle that passes through all the vertices of the polygon.

The first step of this Instructables describes the notation used for expressing the lengths of the various diagonals of a regular polygon having m sides. The next step looks at the relationship between the length of a side of a regular polygon and the radius of the circumscribed circle that passes through all the vertices of the polygon. As in the previous Instructables, before presenting the final equations for the length of the diagonals of any regular polygon we consider the special cases of polygons with 8 and 9 sides (an octagon and a nonagon, respectively).

Step 1: Notation

In the earlier Instructables, the different types of diagonals were defined in terms of the number of vertices of the polygon between the vertices at the ends of the diagonal. We now describe the lengths of diagonals by using a lower case letter l with a subscript as follows:

• l₁ is the length of a diagonal that has one vertex between the vertices defining the two ends of the diagonal (this type of diagonal was previously notated by D₁);
• l₂ is the length of a diagonal that has two vertices between the vertices defining the two ends of the diagonal (this type of diagonal was previously notated by D₂);
• l₃ is the length of a diagonal that has three vertices between the vertices defining the two ends of the diagonal (this type of diagonal was previously notated by D₃);

etc.

As noted in the earlier Instructables, this notation is not a unique description of a diagonal as it depends on whether vertices are counted in a clockwise or anticlockwise direction from the vertex at one end of the diagonal to the vertex at the other end of the diagonal. Thus, for example, a diagonal line is classified as a Dᵢ type of diagonal if i vertices lie between the vertex at one end of the diagonal and the vertex at the other end of the diagonal. However, the number of vertices between the vertices at the ends of a diagonal when the vertices are counted in a clockwise direction may not equal the number of vertices between the vertices at the ends of the diagonal when the vertices are counted in an anticlockwise direction. Thus, if i vertices are counted in one direction and j vertices are counted in the opposite direction, this diagonal was described as a Dᵢ / Dⱼ type of diagonal. In this Instructables, the subscript number associated with the lower case letter l describing the length of the diagonal will be the smaller of the two integers i and j.

This notation allows us to express the length of a side of a regular polygon using the symbol l₀ (the side of a polygon has no vertices present between its ends). It follows that l₀ < l₁ < l₂ < l₃ <....

Step 2: Relationship Between the Length of the Side of a Regular Polygon and the Radius of the Circumscribed Circle That Passes Through All the Vertices of the Polygon

We consider a regular polygon having m sides each of length l₀ and let r be the radius of the circumscribed circle that passes through all the vertices of the polygon. The above diagram shows an isosceles triangle, whose legs represent two radii of the circumscribed circle joining the center of the polygon (the apex of the triangle) to two adjacent vertices of the polygon, and, whose base represents a side of the polygon. The green line between the two radii is an apothem of the regular polygon and is perpendicular to and bisects the side of the polygon.

If we denote the central angle of the polygon by θ where θ = 2π/m, it follows from the above diagram that:

• l₀/2 = r sin (θ/2).

Thus knowing l₀, one can easily find r and vice versa.

In the expressions presented in the following steps, the lengths of the diagonals will be expressed in terms of r which can readily be expressed in terms of l₀ by replacing r with:

• r = l₀/[2 sin (θ/2)].

Step 3: Lengths of All the Diagonals of an Octagon and a Nonagon

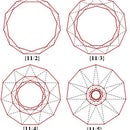
As in the earlier Instructables, we illustrate the procedure described here using an octagon (shown in the above diagram on the left) and a nonagon (shown in the above diagram on the right). The dashed lines show all the radii of the circumscribed circle that join the center of the circumscribed circle to each vertex of the polygon. The red lines in the above diagrams show all the diagonals that can be drawn from one vertex of a polygon (labelled A) to all the other vertices of the polygon (some of these vertices are labelled B, C and D). While the octagon has five diagonals and the nonagon six diagonals, both the octagon and the nonagon have only three different types of diagonals as described in the earlier Instructables.

Each diagonal can be regarded as forming the base of an isosceles triangle whose legs are radii of the polygon's circumscribed circle. As noted in the previous step, the angle, θ, between radii of the circumscribed circle joining each adjacent pair of vertices is equal to 2π/m. If the center of the circumscribed circle is denoted by the letter O, then the angle between the legs of the various isosceles triangles are:

• for diagonal AB, angle between OA and OB = 2θ;
• for diagonal AC, angle between OA and OC = 3θ;
• for diagonal AD, angle between OA and OD = 4θ.

If a perpendicular line is drawn from the center of the circumscribed circle to the base of these isosceles triangles, the angle between the perpendicular line and the legs of the respective isosceles triangles are:

• for diagonal AB, angle = 2θ/2;
• for diagonal AC, angle = 3θ/2;
• for diagonal AD, angle = 4θ/2.

Thus, for the right-angled triangles whose sides are:

• half the base of the isosceles triangle which equals half the length of the diagonal under consideration;
• the legs of the isosceles triangle;
• and, the perpendicular joining the center of the circumscribed circle to the mid-point of the base of the triangle under consideration;

it follows that:

• half the length of the diagonal = r sin (2θ/2);
• half the length of the diagonal = r sin (3θ/2);
• half the length of the diagonal = r sin (4θ/2).

Thus substituting θ = 2π/m, the lengths of the diagonals for both the octagon and nonagon are given by:

• l₁ = AB = 2r sin (2π/m)
• l₂ = AC = 2r sin (3π/m)
• l₃ = AD = 2r sin (4π/m)

Step 4: General Expressions for the Lengths of All the Diagonals of a Regular Polygon

Based on the analysis presented in the previous step, general expressions for the lengths of all the diagonals of even-sided regular polygons having 2n sides (m = 2n) and of odd-sided regular polygons having (2n + 1) sides (m = 2n + 1) are:

• l₁ = 2r sin (2π)/m);
  
• l₂ = 2r sin (3π)/m);
  
• l₃ = 2r sin (4π)/m;
  
• .
  
• .
  
• .
  
• lₙ₋₁ = 2r sin (nπ)/m.