Introduction: A Method for Locating the Images of an Object That Is Equidistant From Two Plane Mirrors Placed So That the Angle Between the Mirrors Is 360/N Degrees, Where N Is an Integer
Physics courses dealing with the properties of reflection in plane mirrors often discuss the number of images formed when an object is placed between two plane mirrors in such a way that the angle between them is 360/n degrees, where n is a positive integer. The location of the images is usually found using the following two facts:
- the image of an object lies in a straight line drawn between the object and the image; .
- the perpendicular distance from the object to the mirror equals the distance from the mirror to the image.
As only a few values for the angle between the two mirrors are usually discussed in these courses (usually, 90 degrees and 60 degrees), no pattern is observed regarding the location of these images.
By systematically using a ruler and protractor to find the reflections of an object placed equidistant from two mirrors for values of n equal to 3, 4, 5, 6, 7, and 8 (for n = 2, the angle is 180 degrees and the two mirrors are equivalent to a single plane mirror), it was found that the object and all its images lie at the vertices of regular polygons. This Instructables shows that when an object and its images are placed in a particular way at the vertices of a regular polygon, such a setup describes the number of images found when an object is placed between two plane mirrors so that the angle between the mirrors is 360/n degrees, where n is a positive integer. This result then provides a general procedure for locating the images of an object placed equidistant from two mirrors where the two mirrors are oriented at angles of 360/n relative to each other.
In the diagrams shown in the following Steps:
- the mirrors are represented by solid red lines that intersect at the centre of various convex regular polygons and bisect two adjacent sides of the polygon; the mirrors are labelled M1 and M2; both these mirrors thus lie on apothems of the polygon; (an apothem is a line from the center of a regular polygon to the midpoint of one of its sides and is perpendicular to that side); imaginary extensions of both solid red lines are represented by dashed red lines;
- the vertex of the polygon at the point of intersection of the two adjacent sides of the polygon through which the mirrors pass is labelled with the number 0; it denotes the position of the object placed so that it is equidistant from the two mirrors;
- the vertex labelled with the number 1 shows the location of the image of the object in mirror 1, and the vertex labelled with the number 2, the location of the image of the object in mirror 2; these images are usually referred to as the primary images of the object in the mirrors;
- the vertex labelled with the numbers 1,2, shows the location of the image in mirror 2 of the primary image labelled 1 acting as an object in mirror 2, and that with the numbers 2,1, the location in mirror 1 of the primary image labelled 2 acting as an object in mirror 1; the images labelled 1,2 and 2,1 are often referred to as the secondary images of the object in the mirrors;
- the vertex labelled with the sequence of numbers 1,2,1 denotes the image in mirror 1 of the image labelled 1,2 acting as an object in mirror 1, and that labelled with the sequence 2,1,2, the image in mirror 2 of the image labelled 2,1 acting as an object in mirror 2;
- the notation used for labelling other images follows the same pattern described in the latter bullet points; thus, for example, a vertex labelled 1,2,1,2,1 represents the image in mirror 1 of the image at vertex labelled 1,2,1,2 acting as an object for mirror 1;
- all other coloured lines joining vertices of the polygon are lines drawn parallel to the sides of the polygon labelled with the numbers 0 and 1 (blue lines), and, 0 and 2 (orange lines); blue lines are perpendicular to mirror 1 and orange lines are perpendicular to mirror 2 (except for the case of an equilateral triangle described in Step 1 below); in Step 3 below, it will be verified that the blue lines are bisected by the red line and its extension representing the position of mirror 1 and the orange lines are bisected by the red line and its extension representing the position of mirror 2; the blue coloured lines represent lines joining an object (or an image acting as an object) to its image in mirror 1 and the lines coloured orange, lines joining an object (or an image acting as an object) to its image in mirror 2.
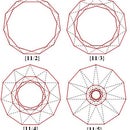
Step 1: Mirrors Placed at an Angle of 120 Degrees
In the above diagram, as noted in the Introduction, the two mirrors are represented by the red lines which intersect at the centre of the equilateral triangle and are perpendicular to two adjacent sides of the triangle. Therefore, from the properties of equilateral triangles, the angle between the two mirrors is 120 degrees. The vertex labelled 0 shows the position of the object that is equidistant from the two mirrors. The vertices labelled 1 and 2 show the location of the primary images obtained when the mirrors are placed so that the angle between them is 120 degrees (the perpendicular distance from vertex 0 to each mirror and the perpendicular distance from each primary image to its respective mirror is equal).
As each of the images labelled 1 and 2 lies on an imaginary extension of each mirror, there can be no further reflections. Thus only two images exist.
Step 2: Mirrors Placed at an Angle of 90 Degrees
In the above diagram, the two mirrors intersect at the centre of the square and are perpendicular to the sides of the square. Therefore, from the properties of a square, the angle between the two mirrors is 90 degrees. If the vertex labelled 0 denotes the position of the object that is equidistant from the two mirrors, then the vertices labelled 1 and 2 denote the primary images formed in the two mirrors. Now:
- the primary image labelled 1 can act as an object that is reflected in mirror 2 resulting in the formation of a secondary image labelled 1,2;
- the primary image labelled 2 can act as an object that is reflected in mirror 1 resulting in the formation of a secondary image labelled 2,1.
Both these secondary images coincide and the vertex where they coincide is labelled 1,2 and 2,1. Thus there can be no further images, resulting in a total of four images.
It should be pointed out at this stage that, when viewing the images with the eye placed approximately equidistant from the planes of a pair of mirrors oriented at an angle of 90 degrees, only three images are seen, with a single image occurring at a point beyond where the two mirrors intersect. It is important to distinguish between the number of images formed and the number of images that can be viewed with the eye. In this Instructables we are counting the number of images that can be formed when two mirrors are placed at particular angles relative to each other.
Step 3: Mirrors Placed at an Angle of 72 Degrees
For a pentagon, the angle between the two mirrors is 72 degrees (360 degrees divided by the number of sides). Note the following argument:
- the line joining the vertices labelled 2 and 2,1 is parallel to the line joining the vertices labelled 0 and 1;
- mirror 1 is perpendicular to the line joining the vertices labelled 0 and 1 and the line joining the vertices labelled 2 and 2,1;
- the length of the side of the regular pentagon with the labels 1 and 2,1 is equal to the length of the side with the labels 0 and 2;
- mirror 1 which bisects the side with the labels 0 and 1, must therefore also bisect the side with the labels 2 and 2,1;
- the distance from image labelled 2 (acting as an object in mirror 1) to mirror 1 is therefore equal to the distance from the image labelled 2,1 to the mirror 1;
- thus the vertex labelled 2,1 can be regarded as the image of the vertex labelled 2.
A similar argument shows that the image labelled 1,2 is the location of the image labelled 1 acting as an object in mirror 2.
This also justifies the statement made in the Introduction, that lines parallel to the side of the polygon which is labelled with the numbers 0 and 1 are bisected by the line and its extension representing mirror 1 and those drawn parallel to the side of the polygon which is labelled with the numbers 0 and 2 are bisected by the line and its extension representing mirror 2. :
In the case of the pentagon, as with the case when two mirrors placed at an angle of 120 degrees, each of the secondary images labelled 1,2 and 2,1 lies on an imaginary extension of each mirror and there are no further images obtained from these secondary images. Thus, four images are formed.
Step 4: Mirrors Placed at an Angle of 60 Degrees
For a hexagon , the angle between the two mirrors is 60 degrees. As in Step 2 when two mirrors were placed at an angle of 90 degrees relative to each other, the tertiary images coincide and the vertex where the images coincide is labelled 1,2,1 and 2,1,2. Thus there can be no further images, resulting in a total of six images.
Again, when viewing the images with the eye placed approximately equidistant from the planes of a pair of mirrors oriented at an angle of 60 degrees relative to each other, only five images are seen, with one image occurring at the vertex where the two tertiary images coincide.
Step 5: Mirrors Placed at an Angle of 51 and 3/7 Degrees
For a heptagon, the angle between the two mirrors is 51 and 3/7 degrees. As with the situations when two mirrors were placed at angles of 120 degrees or 72 degrees relative to each other, images at vertices 1,2,1 and 2,1,2 lie on imaginary extensions of the mirrors, and thus there are no further reflections can be obtained from these images. Thus, there are a total of six images.
Step 6: Mirrors Placed at an Angle of 45 Degrees
For the octagon the angle between the two mirrors is 45 degrees. Both images at vertices 1,2,1,2 and 2.1.2,1 coincide at the one vertex and, as found when the two mirrors were oriented at an angles of 90 degrees or 60 degrees, no further reflections are obtained, resulting in the formation of 8 images.
Step 7: Some Observations Made From Examining the Previous Steps
Note the following:
- all the reflections of the object as well as the object itself lie at the vertices of a regular polygon;
- an image labelled with the number 1 or labelled with a sequence of numbers that ends with the number 1 acts as an object in mirror 2 to result in an image labelled with a sequence of numbers that ends with the numbers 1, 2;
- an image labelled with the number 2 or labelled with a sequence of numbers that ends with the number 2 acts as an object in mirror 1 to result in an image labelled with a sequence of numbers that ends with the numbers 2,1;
- when the mirrors are placed at an angle 360/n where n is an odd integer, each of the final two reflections results in images lying on an imaginary extension of one of the mirrors; the total number of images formed is one less than the number of vertices (one of the vertices is occupied by the object);
- when the mirrors are placed at an angle 360/n where n is an even integer, each of the final two reflections result in images that coincide at a vertex lying between the extended lines representing the two mirrors. This final image is equidistant from the extended lines representing the two mirrors; the total number of images formed is equal to the number of vertices;
- images labelled with the number 1 as well as images labelled with a sequence of numbers that ends with the number 1 lie at vertices on the same side of the regular polygon that is bisected by mirror 1;
- images labelled with the number 2 as well as images labelled with a sequence of numbers that ends with the number 2 lie at vertices on the same side of the regular polygon that is bisected by mirror 2.
Step 8: A Procedure for Locating and Labelling the Images Obtained When an Object Is Placed Equidistant From Two Mirrors That Make an Angle of 360/n Degrees With Respect to Each Other
Preliminary steps:
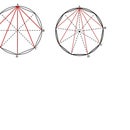
- draw a polygon with n sides and thus n vertices (a 12 sided polygon, a dodecagon, is shown in the above diagram);
- choose a vertex at which to place the object and label this vertex with the number 0;
- draw two lines to represent the mirrors (and their extensions by dashed lines), so that the two lines (and their extended dashed lines) pass through the centre of the polygon and bisect the sides of the polygon which are common to the vertex chosen as the position of the object; label the mirrors M1 and M2;
- label the vertex showing the primary image of the object reflected in mirror 1 with the number 1 and the vertex showing the primary image of the object reflected in mirror 2 with the number 2;
- draw lines parallel to (a) the side of the polygon with labels 0 and 1, and (b) the side of the polygon with labels 0 and 2
A series of steps for locating the remaining reflections:
Start by performing the following two steps:
- at the vertex labelled with the single number 1, follow the line that is parallel to the side of the polygon with labels 0 and 2, and where it meets a vertex of the polygon label this vertex by adding the number 2 to the number 1; the vertex is now labelled with the numbers 1,2;
- from the latter labelled vertex, follow the line that is parallel to the side of the polygon with labels 0 and 1, and where it meets a vertex add the number 1 to the numbers so that the string of numbers ends with the number 1; the vertex is now labelled with the numbers 1,2,1.
Repeat an analogous two steps for each vertex where the label is a series or string of numbers ending in the number 1; that is:
- follow the line that is parallel to the side of the polygon with labels 0 and 2, and where it meets a vertex of the polygon label this vertex by adding the number 2 to the string of numbers;
- from this latter labelled vertex, follow the line that is parallel to the side of the polygon with labels 0 and 1, and where it meets a vertex add the number 1 to that the string of numbers so that the string of numbers ends with the number 1.
Continue this process until either the vertex of the polygon opposite the vertex labelled 0 (for n even) or the vertex at the side of the polygon opposite the vertex labelled 0 (for n odd) is reached.
The vertex with the label 2,1 is found by starting at the vertex labelled with the single number 2: follow the line that is parallel to the side of the polygon with labels 0 and 1, and where it meets a vertex of the polygon label this vertex by adding the number 1 to the number 2; the vertex is now labelled with the numbers 2,1;
For the situation where two images coincide, only one of them is labelled when the above steps are followed. In order to label the second image start with the longest string of numbers ending with the number 2 and follow a line parallel to the side of the polygon labelled 0,1 and where it meets a vertex add the number 1 so that the string of numbers ends with the number 1.
An application of the above steps is shown for a regular dodecagon in the two diagrams above. The diagram at the left shows the end result after carrying out the preliminary steps; the other diagram shows the end result after carrying out the steps for locating the remaining reflections (for clarity, colours have been added to this diagram).
The latter subheading used the indefinite article a (A series of steps...) since the above steps could have been described by interchanging the numbers 1 and 2.