Introduction: Transistor Basics - MOSFETs
(First of all, I made some edits to the HTML code for this I'ble, which is optimized for the desktop site, so it may not be ideally viewed on a mobile device.)
Transistors are arguably the most important electronic component in use today. They are nearly everywhere, in nearly every electronic device we use. Radios, phones, computers, game consoles, TVs, cars, toys ... the list goes on. Without them, life would be drastically different.
The idea of the transistor was first developed and patented in 1925 by Julius Edgar Lilienfeld, but manufacturing techniques for the required materials weren't good enough to produce a high enough quality crystal and so development and testing came much later. William Shockley, John Bardeen and Walter Brattain of Bell Labs spent many years and LOTS of money researching and developing what became the point-contact transistor, which was a PNP type transistor and was successfully demonstrated as a voice amplifier on 23 Dec, 1947. It wasn't until 1950 that Shockley developed the bi-polar transistor (BJTs) that became so ubiquitous, and still is today. For some practical applications of BJTs, see my BJT Instructable.
Julius Lilienfeld had actually described what we know now as the field effect transistor, or FET (more specifically he predicted the JFET), in his patent of 1925, and it was the FET that the guys at Bell Labs were trying to produce when they developed the point-contact transistor. It wasn't until 1960 that the first MOSFET was introduced by Dawon Kahng and Martin Atalla.
MOSFETs differ from BJTs in that BJTs require that a current be applied to the base pin in order for current to flow between the collector and emitter pins. On the other hand, MOSFETs only require a voltage at the gate pin to allow current flow between the drain and source pins. MOSFETs actually have a very high gate impedance by design, which makes them very good at reducing the amount of wattage a circuit requires to run. One of the first transistor based computers required 150 watts, but it used point-contact transistors. That doesn't seem like much compared to now, but it only had 200 transistors and 1300 diodes. My dad's Casio watch from 1990 had more computing power and didn't require nearly that much power. (Thank goodness. Can you imagine the burn marks?) Thankfully computers now use MOSFETs almost exclusively in their designs, so they don't require as much power.
As indicated by the title, I will be going over some uses for MOSFETs in this Instructable. This is not intended to be an exhaustive resource, simply a "get started" point so you can get on building.
Step 1: Parts and Some Theory
There are lots of different types of MOSFETs out there, so picking a specific one to use can be a little bit overwhelming. For the projects here I will be using ZVP2110A (datasheet) and ZVN2110A (datasheet) for pretty much everything. They are a bit outdated, but more than adequate for our purposes here. The ZVP is P-channel, meaning that it requires a relatively negative signal at the gate pin to function. The ZVN is N-channel, requiring a relatively positive signal to function. I know it seems backwards, but if you think of negative as "holes" and positive as "plugs", you can't make "holes" and "holes" work, you need "holes" and "plugs" to have a smooth "surface" over which the electrons can flow.
The image below shows the two types of schematics symbols associated with MOSFETs. (It should be noted here that the schematics shown are only for enhancement type MOSFETs. There are also depletion type, and the difference is that enhancement "turn on" when voltage is applied, whereas the depletion type "turn off". We will deal only with enhancement types here.) The three pins are labeled Gate, Drain, and Source. (FYI - for BJTs, these are labeled Base, Collector, and Emitter and serve the same basic functions). Carefully note the orientation of the three pins. It's very easy to switch the MOSFET around backward, so always double check your datasheets for the MOSFET you are using to ensure the correct pin orientation. The ZVNs and ZVPs that I'm using have a different pin orientation than most MOSFETs that use the TO-220 package.

Take a look at the datasheet again for the ZVN2110A. As always there is a lot of information on the datasheet. Pay close attention to maximum ratings. Always give yourself some room between operating and max values and stay well away from max values. When you operate near max values, you generate more heat than is needed, and you will lose performance as well as shorten the life of the transistor. Get a transistor with a higher rating if needed.
In order for N-channel MOSFETs to work, the gate voltage (VG) must be more positive than the source voltage (VS). This is often noted as VGS and a frequent minimum value for VGS is 0.6-1.0V. Note that according to the datasheet, the ZVN can handle a VGS of +/-20V, but it only takes between 0.8V (min) and 2.4V (max) to open the gate. This means that you can apply the same supply voltage to the gate as well as the drain of your MOSFET without worrying about performance issues. That will make more sense later on.
Another factor to keep in mind is the drain-source voltage (VDS). VDS cannot be less than VGS or the MOSFET simply won't work.
For P-channel MOSFETs, we need to invert all of the above. VDS should be the most negative value, VS should be the most positive value, and VGS should be less than VS but higher than or equal to VDS.
For more on MOSFETs, check out these pages at electronics-tutorials.ws and allaboutcircuits.com
Step 2: A Simple Switch
MOSFETs are really easy to "saturate", which just means that they are fully open, and they are dead reliable for very fast switching between their saturation and cut-off regions (fully on and fully off regions). This makes them wonderful switches, especially for high power applications like motors, lamps, etc. In most cases, you can use the same power supply that you are using for your high power device to operate the MOSFET as well, using a mechanical switch to apply the gate voltage. The image below shows exactly that type of application. (Alternatively, you can also use an electronic signal, like from a microcontroller, to activate the MOSFET. This is extremely common, and useful, since the output pins on microcontrollers are not designed for high power applications. Also, be sure to check the gate threshold voltage for the MOSFET and compare it to the microcontroller output pin voltage. Some MOSFETs require more voltage than some microcontrollers can output.)

Build: Place the N-ch MOSFET on the board. Connect the 1kΩ resistor between the gate and GND. Connect the switch between the gate and +9V. Place the 220Ω resistor and LED in series between +9V and the drain. Tie the source pin directly to GND. See image below.

Push the button and the LED should light up. The 1kΩ resistor acts as a pull-down resistor, keeping the voltage at the gate at the same potential as the negative battery terminal until the button is pushed. This puts a positive voltage at the gate, opening the channel between the drain and source pins and allowing current to flow through the LED. Note that the gate voltage is +9V and there are no negative side effects.
Now let's see how we connect a P-ch MOSFET. Remember that the relative positive/negative values for the gate, drain, and source are inverted here. See schematic below.

Build: Place the P-ch MOSFET on the board. Connect the 1kΩ resistor between GND and the gate. Place the switch between -9V and the gate. Place the 220Ω resistor and the LED in series between the drain and -9V. Connect the source directly to GND. See image below.

Allow me to digress for a moment because the connections here seem weird, I know. (If this already makes sense, just push the button.) Instead of using the positive side of a 9V battery as +9V, we are using it as GND and the negative as -9V. But remember, GND is arbitrary and relative, which can be really confusing. You get to set it where you want it so that it makes sense. So let's look again at what we are building.
Look again at image 3, the schematic. Remember that for a P-ch MOSFET, we need the source to have the highest relative value, the drain should have the lowest relative value, and the gate lower than the source, but greater than or equal to the drain. We know that the positive terminal on a 9V battery is 9V more positive than, or relative to, the negative terminal. By saying "more positive" we can start to get out of the +9V/GND box and start to think more relatively. We can also correctly say that the negative terminal is 9V more negative relative to the positive terminal. We can now give either terminal any value we want and the relation between the two stays the same. That's the important part. As long as the more negative terminal on the battery is connected to the pin that needs the more negative value (the drain), and the more positive terminal is connected to the pin that needs the more positive value (the source).
Anyway, back to the circuit. Push the button, the LED comes on again.
Again, using these with a microcontroller, all you need is the correct relative signal paired with the correct MOSFET and you get very useful high current drivers.
Step 3: Motor Drivers
Building off of Step 1, we can use the ZVN as a DC motor driver. To avoid over-current damage to the ZVN, I'm using a small 6V DC hobby motor, much like the kind you find inside of small hobby servos. With a higher current N-ch MOSFET, you can drive larger motors with larger current needs.
Looking at the schematic below you'll see two diodes placed backward (reverse biased) across the motor contacts and across the MOSFET drain/source pins. Any electrical component that has a coil in it (inductors, relays, solenoids, motors, etc.) can generate a very large voltage spike in the reverse direction when it is turned off. (This is a common problem in airsoft, and it can lead to premature wear on the trigger contacts that turn on the motor. An easy fix for this is to add an "airsoft MOSFET", and this is a similar example. It should be noted that the parts used here are nowhere near capable of handling the voltage/current needs of an airsoft motor, so don't use this specific example.) The diodes give that spike a place to go so that the components are not damaged.

Build: Place the ZVN on the board. Connect the 1kΩ resistor between the gate and GND. Connect the switch between +6V and the gate. Connect the source to GND. Connect the drain to the negative motor lead. Tie the positive motor lead to +6V. Place one diode between the drain and source pins, with the stripe on the diode facing the drain pin. Put the other diode across the motor leads, with the stripe toward +6V. See image below.

Once everything is connected, double check it. And again. It's really easy to get things switched and even though it probably won't matter with this circuit, it's a good habit to already have when it does matter. Then push the button and your motor should run in one direction.
To switch direction, we can simply swap the leads to the motor, but that would be impractical in a real project. Well, if an N-ch MOSFET turns the motor in one direction, a P-ch MOSFET should turn it the other way, right? Let's see what that looks like below.

Build: Place the ZVP on the board. Connect the 1kΩ resistor between the gate and +6V. Connect the switch between GND and the gate. Connect the source to +6V. Connect the drain to the negative motor lead. Tie the positive motor lead to GND. Place one diode between the drain and source pins, with the stripe on the diode facing the source pin. Put the other diode between GND and the drain, with the stripe toward he drain. See image below.

Push the button and the motor should spin in the opposite direction.
Either of the schematics in images 1 and 3 would work really well with a microcontroller PWM signal in place of the switch. This would allow for speed control instead of just fully on/off.
Now let's do a thought exercise. Look again at image 3. What happens if I move the GND reference from the negative battery terminal to the positive? How does it change the build instructions? The answer is that it doesn't change the build sequence one bit, just how you look at the reference voltages. Specifically, we replace all "GND" references with "-6V" and all "+6V" references with "GND". We can do the same thing with the schematic and instructions associated with image 1. It's important to remember that the idea of "more positive" and "more negative" don't change if we do that.
The reason I bring that up is this. What if we need a motor controller that can go in both directions? We already have two circuits that can each go in one direction, opposite to each other. How do we combine them? We are going to need +/- power supplies, but images 1 and 3 show only +6V. How do we resolve this? See image below. (For this circuit you will need + and - power supplies, with a GND reference equidistant between them. Since my motor is 6V, I have +/- 6V. The build image shows 9V batteries, but fritzing doesn't have 6V battery images, so I made do.)

Build: Connect one positive battery lead to the positive power rail. Connect the negative battery lead from the other battery to the negative power rail. You should have a loose positive lead and a loose negative lead. Connect them together in the same row on the breadboard. This point is now your GND reference. Now place the ZVN and ZVP MOSFETs on the board with no pins connected. Connect both switches separately between GND and each gate. Connect one 1kΩ resistor between -6V and the gate of the ZVN. Connect the other 1kΩ resistor between +6V and the gate of the ZVP. Tie the source of the ZVN to -6V and the source of the ZVP to +6V. Tie the two drain pins together. Place one diode across the ZVN source/drain pins, with the stripe toward the source pin. Place the second diode across the ZVP source/drain pins, with the stripe toward the drain pin. Connect the negative lead on the motor to the drain pins, and the positive motor lead to GND. See image below.
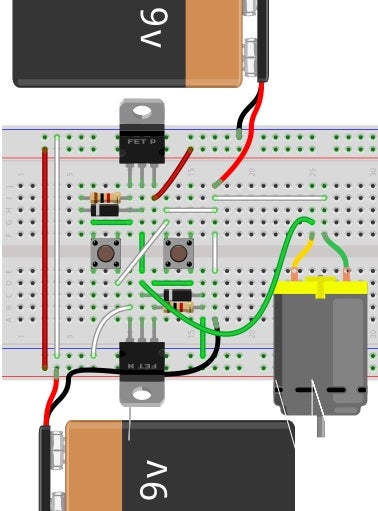
Now push each button, but not both at the same time. The motor spins one way for one button, and reverses direction for the other button. You can swap the momentary switches with slide switches so the motor stays on, but again, do not turn on both switches at the same time.
Another bi-directional motor controller is called an H-bridge, and I will leave you to explore that idea more.
Step 4: Logic Gates
Now let's look at how MOSFETs are used in logic computations.
Well, let me back up a step. In order to understand computing, you must have a basic knowledge of boolean algebra. If you are unfamiliar with boolean algebra, stop here and do some research. I'll try and simplify it, but electronics-tutorials.ws has a great set of lessons on it specifically targeted to electronic, or digital, logic. The BBC has a cool interactive site for learning digital logic as well. Digital logic is what we use to design computer logic processors. You may also want to learn more about K-maps, which allow you to see complex truth tables in a different (and often easier) way, and De Morgan's theorems, which are the foundation of boolean algebra. In a broader sense, reference material in discrete mathematics, which covers logic but also set theory, recursion, and relations, may also come in handy. Wikipedia has a list of operators that are commonly used for logic expressions. Also, by way of clarification, in digital logic we use 1's (on) and 0's (off) to indicate the state of the input or output.
NOW let's look at how MOSFETs are used in logic computations, shall we.
The first logic gate I want to introduce is the two-input AND gate because it's probably the easiest logic to understand. The image below shows the schematic symbol for an AND gate.

The output of the AND gate will only be high if BOTH of the inputs are also high. If either input is low, the output is also low. The symbol (in digital logic) is "●". See the table below for the AND gate truth table.
| A | B | A • B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
When looking at truth tables, the number of possible outcomes in the far right column is related to the number of inputs by raising 2 to a power equal to the number of inputs. In other words, if you have two inputs, you have 22 = 4 outputs. With 3 inputs, you get 23 = 8 outputs, and with 8 inputs your get 28 = 256 possible outputs.
The second gate to consider is the NAND gate, or Not AND. NOT is the way we describe negation, or saying something is the opposite. The negation of true is false, and the NOT of AND is NAND. The symbol for NOT (in digital logic) is the tilde, "~". The NAND truth table is similar, but opposite to the AND truth table. See below.
| A | B | ~(A • B) |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
The output column is the complete opposite of the AND truth table output, isn't it? Other truth tables (and gates as well) are OR, NOR, XOR, XNOR, and NOT. I'll refer you to this page for a comprehensive list of truth tables used in digital logic and the associated schematic symbols.
So how do MOSFETs come in to play with logic gates? Well, since MOSFETs are so easy to saturate (turn fully on) with a low voltage and almost negligible current, we can build the logic gates above with them and in turn build extremely reliable digital logic systems to process data. Let's look at how a NOT gate looks on the inside and see if we can make some sense of this. I'm starting with the NOT because it takes the fewest number of MOSFETs to build and should therefore be less confusing. See the schematic below.
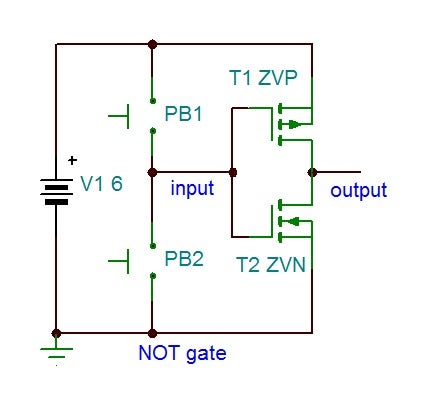
The NOT gate is used, as it's name implies, to negate or invert the input signal. PB1 connects the two MOSFET gates to +6V, but only the ZVN will open with positive voltage. When it opens though, it connects the output to GND, so the + input becomes GND at the output. Conversely, when we apply GND to the input through PB2, only the ZVP opens, which connects the output to +6V, again inverting the signal. (When neither button is pressed, the output can 'float' and be either +V or GND, so it's common to force the input to one state to guarantee that you know what the output is at that moment in time. A simple way to do this is to replace either of the buttons with a 1kΩ resistor, forcing the input to that potential when the remaining button is not pressed. You get to choose which state is your idle state this way.) I encourage you to build this, but I won't detail the instructions.
Now let's see what a NAND gate looks like inside. This time we are using 4 MOSFETs. See the schematic below.

The LED will only turn off (logic 0) when both SWA and SWB are high (logic 1). (Notice how the LED symbol in the schematic is nearly black, indicating off? Remember that.) Compare this result to the NAND truth table. Again I encourage you to build this, but I will not be including build steps.
What do we get when we mix the two? If the NAND is a NOT AND, and we combine it with a second NOT, what do we get? Isn't that just a double negative? So the NOTs cancel, logically, and we're left with an AND gate. In boolean algebra, the equation looks like ~(~(A●B))⇔(A●B). Pretty neat. Below is the truth table for that in case that makes it easier to understand. Also below is the schematic, to which I've added some labels for clarification.
| A | B | (A • B) | ~(A • B) | ~(~(A • B)) |
|---|---|---|---|---|
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 |

If you compare the schematics for the AND, NOT and NAND gates, you'll see that even though on the outside the NAND is the negation of AND, on the inside the AND gate is actually made of a NAND gate followed by a NOT gate. So like I said above, the AND gate is actually a NOT NAND. Don't worry, it took me a while to catch on to that one too. Also, notice how the LED in the schematic is bright red, indicating that it is on when the switches are on. Compare that to the NAND gate schematic image above.
Below are schematics for the OR and XOR gates. Notice that both are actually a combination of their respective inverse (NOR and XNOR) with a NOT gate.


In truth it can be proven that any logic gate, and therefore any logic circuit, can be built with some finite number of NAND gates. Also, FPGA chips and the boards designed around them allow you to write code (using VHDL or Verilog) that will connect the gates as needed in order to complete the circuit and are a very easy way to start building and implementing digital logic circuits. Considering how difficult it can be to wire up just one logic gate, can you imagine trying to wire up an entire logic circuit using discrete MOSFETs? It's only been possible in the last few years for students and hobbyists to be able to build circuits like adders, which are simple in theory but complex to build, because of the advancement of technology and the miniaturization of the parts involved. Anyway, I digress. I'm just so grateful for the technology that is at our fingertips, when not that long ago it was only a wish.
So now that it's as clear as mud, let's move on. Now that we have gates, what can we do with them?
Step 5: Logic Circuits
The circuits here will be very simple, but will require either a LARGE number of discrete N-ch and P-ch MOSFETs or logic ICs. Logic ICs are cheap and easy to find (try this link for the 4001 IC or this link for the 7402 IC, which are both quad NOR gates), so it won't be too difficult.
The circuits came from Forrest Mims book Digital Logic Projects: Workbook II. Here's a link to the PDF from RadioShack, or to Amazon.com for purchase. (As a side note, I recommend getting Basic Electronics: Transistors and Integrated Circuits: Workbook I as well, also from Forrest Mims. Amazon.com or PDF)
Some things to remember when working with logic ICs:
- Be sure to avoid any static buildup or discharge to avoid damaging the chips.
- Each chip has a common pin for +V and a common GND pin. These are not shown on the schematics, but should be easy to find on the datasheet (7402 datasheet).
- Any input pins that are not being used should be connected to GND. This will also not be shown on the schematics.
- Logic chips are not meant to be high current drivers for large loads like motors and such. However they can be used for small loads, like an LED, or to provide the signal for such drivers, like in step 3
For the following schematics, note the SN74XX number above each gate. That is the IC number I used to build the circuits if you want to get some ICs and build these on your own. Most of these chips come with 4 of the specific gate, so the SN7402 below would have 4 NOR gates.
OK, let's begin with a simple LED flasher. Using just two NOR gates, we can build an oscillator. See schematic below.

LED2 and R4 are optional if you want to have two LEDs that flash back and forth. Otherwise LED1 will flash on/off at a rate determined by the values of R1 (try a potentiometer here) and C1.
The next circuit is a set/reset latch, which is a key component of sequential logic. Latches form the basis of computer memory, since the output remains on/off even after you release the switch. A group of 8 latches would form the core structure for an 8-bit memory cell. In memory, the SR latch is known as a D latch (data) and is used with the system core clock to determine when to latch. (There is more to it, but it's beyond the scope of this I'ble. Look here for more on how computer memory works, and here for a comparison between sequential and combinational logic.) Now, the schematic.

This circuit is more of a demonstration of concept since we are usually only interested in one output from the latch because as the outputs flip-flop between states as the buttons are pressed, they will always be at opposite states to each other. You can tie one of the outputs here to a second circuit and use the latch as a "push on/push off", non-mechanical switch for the second circuit.
As mentioned before, any logic gate or circuit can be made from a finite number of NAND gates. Here's an example of an OR gate made with 3 NAND gates.

To change the OR to a NOR, add a fourth NAND between the output of U3 and the LED, with the two inputs of U4 tied together.
It seems like it would be more costly to use a lot more MOSFETs to do the same thing (4 for 1 NOR gate, 16 for 3 NAND gates) and when you are designing a new chip, space and the number of parts in that space is the most important thing regarding the cost of the chip. Well, here is the benefit. Remember the FPGA chips I mentioned before? These are generic chips that can be programmed for any situation. If we have a huge bin of NAND gates that can make anything, then we can make... anything. But if we try to conserve space and costs by using specific gates, we are limited by the number of each gate we have. What happens when we need more OR gates? Sounds like a redesign to me, and that costs money too. The point is that if you have a specific design already in mind, it may be better to use the exact gate needed and not a bin of generic NAND gates. But if you are prototyping and designing from scratch, you need flexibility, and that is where NAND gates shine.
Anyway, back to it. Again using only NAND gates, we can build an XNOR gate.

By removing U5 and tying the output of U4 to R3, we get an XOR gate.
A single XOR gate can be used as a 1 bit binary adder. By adding two NAND gates (which is just an AND gate if you remember), we get a half-adder with a two bit output.

A full-adder requires a couple of changes (add an XOR, two NANDs, and an OR gate), which add an input to handle carry-in signals from a previous adder. Several adders are then stacked together, one adder for each bit, to build an adding machine. It's actually pretty elegant. Below is a full-adder circuit.

PB1 is bit A, PB2 is bit B and PB3 is the carry bit from the previous adder block. If we only press PB1 or PB2, we are adding 1+0 and only LED 2 will light to indicate a value of 1. If we press PB1 and PB2 together, that indicates a binary addition of 1+1, which is 10 in binary (indicated as 10b). That will light up LED1 and leave LED2 off. If we then press PB3 and add 1 more, we get 11b, and both LEDs light.
Below is a block diagram for a 4-bit adder using 4 full-adder blocks. The first block on the right (with A0 and B0) can be swapped with a half-adder with no effect on the output. It simply removes the the carry-in (Cin) on the first full-adder, which is connected to GND here anyway.

In this example we are adding two, 4-bit numbers A and B. The first bits of each (A0 and B0) are added on the right, with the result sent to S0 and any carry bit (C1) sent to the next adder. A1 and B1 are then added, along with C1 from the first adder, the result goes to output S1, and any carry bit is sent on (C2). The last adder either displays the final carry-out bit (C4), if any, or ignores it if there is no room or if it is unimportant. You the designer get to make that decision.
Let's look at one more logic example, a 4-bit comparator digital lock. As mentioned, XOR gates can be used as adders, but they are also comparators, outputting one state if both inputs are the same, and the inverted state if both inputs are different. This allows us to check the state of a pin and switch and output only if it is correct.

The pins labeled 1, 2 , 3, and 4 are for programming the lock. You set these pins high or low to determine the combo, and then you have to press the same corresponding buttons PB1-PB4 in order for the output of U13 to go low. This allows current to flow through the LED and it turns on. To set the combo you can either tie the pins directly to GND or +V, or use some sort of memory device that will store the input once set and not change. Sound familiar? Yep, you can easily add a latch circuit to the 4 combo set pins. As long as the latches don't lose power, they will not lose the value stored in them. The applications for this are simple at best, but it gets the idea across. (I am in no way responsible for how you choose to use this circuit as it is not really secure and can be easily hacked/reset.)
Step 6: Conclusion
As you can see MOSFETs are extremely useful. They are arguably the most important electronic component in use today when you look at how much we rely on them for our everyday electronic devices. There isn't a day that goes by that you don't use several million transistors just to do something simple, like look at what time it is. Or make your coffee, check your email, watch a movie, listen to music, or read this I'ble.
You may have noticed that there is no mention of MOSFETs as amplifiers here. I did that on purpose, but that isn't to say that they can't be used as such. My experience has been that analog signal amplification duties are best handled by BJTs, and fast, high current switching is best done by MOSFETs. I realize that is a generalization, as there are plenty of examples for both transistor types working both ways very well. I encourage you to do the research yourself if you wish to learn more on those applications.
Thanks for reading. Please don't hesitate to ask questions in the comments below. You never know when someone else has the same question and that way we can all learn and help each other get better. Have fun building!
Also, please check out the Digilent blog where I contribute from time to time. And please vote for me in the LittleBits Tech Contest. Thanks!
Last thing: a huge shout out to I'bler nodcah for his amazing I'ble on how to enhance your own I'bles by editing the HTML code. Go check it out!

Participated in the
Tech Contest











