Making a Model That Illustrates Partitioning a Cube Into Six Congruent Tetrahedra

This Instructables can be regarded as an extension of an earlier Instructables, which resulted in the partitioning of a cube into 24 congruent mirror-image tetrahedra. The current Instructables was undertaken after reading an article on the web that describes partitioning a cube into six mirror-image congruent tetrahedra. The article points out that, for most people, visualizing such a partitioning from a two dimensional diagram is not easy (http://puzzling.stackexchange.com/questions/12838/partition-a-cube-into-6-congruent-tetrahedra). While there is a YouTube demonstration of this partitioning (e.g.,see: https://www.youtube.com/watch?v=ffnVCEAcOns), a better appreciation of this problem is obtained by building an actual model illustrating the partitioning.

In the previous Instructables, six diagonal planes of symmetry of a cube were assembled together starting with two rectangular planes slotted together along cuts made parallel to the shorter side of the rectangle. Since the present construction requires three such rectangular planes to meet at two diametrically opposite vertices of the cube, the first two planes must be slotted together with cuts made along one of the diagonals of each of the rectangular planes. The third rectangular plane is cut into two right angle triangles. In order for the hypotenuse of these right angled triangles to lie along the intersection of the first two rectangular planes, the right angle triangles as well as the first two planes require some support to hold them in their correct orientation (when viewing the three planes of symmetry along their common diagonal, each of the planes should make an angle of 60 degrees relative to each other.) The support suggested here is provided by two opposite external square faces of the cube. In order to clearly observe the final construction, the two squares are made from transparent flexible plastic, which can be readily obtained from discarded food containers. Beside the two pieces of transparent flexible plastic, the only other materials needed to illustrate this construction are those used in the earlier Instructables, namely: three different coloured pieces of cardstock, plane uncoloured cardboard for constructing tetrahedra (cardboard from a cereal box was used here), scissors, clear sticky tape and a pencil or ballpoint pen

Step 1: Drawing and Cutting

Cut two squares from the two pieces of clear flexible plastic. The side length of the squares should equal the length of the side of the final cube that is to be constructed. One way to cut the square pieces of plastic is to draw the required square on a piece of paper, attach it with sticky tape onto a plastic sheet and cut the plastic with scissors, following the lines of the square that appear on the paper through the plastic sheet.

Cut three rectangles from the three different coloured pieces of cardstock. The length of the sides of the three rectangles should be in the ratio of 1 to √2 with the shorter side of the rectangle having a length equal to that of the length of the side of the final cube that is to be constructed.

Draw on each rectangle one of its diagonals.

Cut one of the rectangles along its diagonal so as to form two right angled triangles.

On each of the two remaining rectangles cut a slit with each slit starting from a vertex of the rectangle and finishing one half of the way along the diagonal from where the cut began. When cutting slits, try and keep the width of the slits just under 1 mm.

Step 2: Attaching Triangles to Transparent Faces of the Cube

Using sticky tape, attach each right angled triangle to one of the plastic squares so that the longer side that is adjacent to the triangle’s hypotenuse is placed along a diagonal of the square (the vertices of this side of the triangle should touch opposite vertices of the square)

Step 3: Final Assembly

Slide one rectangle into the other one along the diagonal slits made in them. Try and keep the planes of the two rectangles at an angle of approximately 120 degrees / 60 degrees to each other when viewed along their common diagonal.

Using sticky tape, attach the shorter sides of each rectangle to adjacent sides of the square pieces of plastic so that the hypotenuse of each triangle lies along the common diagonals of the two rectangles. This should fix the angle between the two rectangles at 120 degrees / 60 degrees to each other.

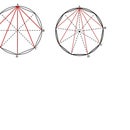
Step 4: Analysis of the Geometric Figures That Result When a Cube Is Partitioned Along Three Diagonal Planes of Symmetry That Meet at Two Diametrically Opposite Vertices

Look directly down on the faces of the cube and, except for the two faces of the cube with an attached plastic square, assume that all faces of the cube are present. One then sees that each face has on its surface two adjacent tetrahedra with two faces of each tetrahedron at right angles to each other. Note also that all four faces of the tetrahedra are made up of right-angled triangles. Thus the original cube could be reconstructed from six such tetrahedra.

These tetrahedra while congruent are not identical. Three of the tetrahedra are mirror images of the other three. The above photos show two such mirror-image tetrahedra inserted into one of the cube’s faces. Two different views of the mirror-image tetrahedra are also shown in the above photos.

The construction of these tetrahedra is described in the next step.

Step 5: Step 5: Construction of Tetrahedra

The tetrahedra shown in the photos in the previous Step were constructed as follows:

• Draw on plane cardboard and cut out two squares and two rectangles whose dimensions are a couple of millimetres less than that used in Step 1 (in order to account for the thickness of the cardboard stock used in Step 1).
• Draw diagonals on the squares and rectangles; in the case of the rectangles, draw the diagonals so that if on one rectangle the diagonal starts at the top left-hand vertex and finishes on the bottom right-hand vertex, on the other rectangle the diagonal starts at the top right-hand vertex and finishes on the bottom right-left vertex.
• Cut both squares along their diagonals.
• Make a fold in the rectangles along their diagonals and then flatten them out again.
• Attach using sticky tape the longer sides of the triangles to the longer sides of the rectangles to obtain two non-regular hexagons having equal side lengths, two opposite right angles and two opposite pairs of angles of 135 degrees as shown in the above photo.
• Finally, fold the two hexagons so as to form two tetrahedra and use sticky tape to keep the faces of the tetrahedra in their correct configuration.

Step 6: A Further Observation

Note the relative dimensions of the sides of the triangles that make up the four faces of the tetrahedron relative to the length of the edge of the cube which is taken as 1. The relative lengths of the sides of the triangles making up the four faces are:

1. Two triangles with dimensions: 1, 1, √2;
2. two triangles with dimensions: 1, √2, √3.

The four triangular faces of the mirror-image tetrahedra in the previous Instructables are:

1. Two triangles with dimensions: 1/2, 1/2, √2/2;
2. two triangles with dimensions: 1/2, √2/2, √3/2.

Those in the previous Instructables have dimensions one half of those found here. Thus the two sets of tetrahedra are similar.

In agreement with this observation, note the following:

Arrange any one of the mirror image tetrahedra so that one of the two faces that are at right angles to each other (one of the isosceles right angled triangles) forms the base of the tetrahedron. Then the other right angle isosceles triangle provides an edge that is at right angles to the base of the tetrahedron. This edge provides a measure of the height of the tetrahedron. Then using the formula for the volume of a tetrahedron (volume = 1/3 x area of base x height) the volume of each tetrahedron in the construction given in this Instructables is1/6 whereas that in the previous Instructables is 1/24. These volumes are based on the relative dimensions of the sides of the triangles that make up the four faces of the tetrahedron given above.

Thus a cube of unit volume can be constructed from 6 mirror-image tetrahedra as discussed in this Instructables or from 24 mirror-image tetrahedra as described in the previous Instructables.