Introduction: Behaviour of a Refracted Ray of Light When It Touches Adjacent Sides of a Glass Prism Vs. a Water Prism
One of the simplest experiments performed by students studying refraction of light uses a rectangular glass prism and four pins. Two of the pins are placed in an upright position so that the holes made by their tips through a piece of paper when joined by a straight line represent the path taken by the incident ray (the paper is placed over some material like cork or corrugated cardboard). The other two pins are placed so that all four pins are in line with each other when viewed through the opposite face of the glass prism to that through which the incident ray entered. The line obtained by joining the holes made by the tips of the latter two pins represent the path taken by the emergent ray emanating from the opposite face of the glass prism.
Unlike the experiment usually performed by students, this Instructables looks at the conditions required for an emergent ray to emanate from the surface of a rectangular prism at right angles to the surface through which the incident ray entered the prism. The steps below show:
- that it is not possible using a glass prism of refractive index 1.5 (an approximate value for crown glass) to view an emergent ray through a surface at right angles to the surface through which the incident ray entered the prism;
- that if we have a rectangular water prism (i.e., a thin-walled transparent rectangular container made of glass or Perspex filled with water) of refractive index 1.333 (the quoted value for water in the literature) then, for a restricted range of values for the angle of incidence, it is possible to view the emergent ray through a surface at right angles to the surface through which the incident ray entered the prism (in this case it is assumed that the thin walls of the container do not significantly modify the path of the incident and emergent rays; a justification for this assumption is provided in the last Step of this Instructables).
For readers not familiar with some of the concepts used in this Instructables, namely, reflection, refraction, Snell's law, and critical angle, refer to these articles and these articles in The Physics Classroom.
I wish to thank Professor Philip Kuchel and Dr Dan Montague for the helpful comments made regarding this Instructables and all earlier Instructables that I have written.
Step 1: One Way to Look at the Problem
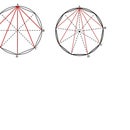
The top diagram above shows what typical results look like for the simple experiment carried out by students. PQRS represents the rectangular prism. Line AB in the top diagram above represents the incident ray. The pins which are placed to represent this ray are positioned in such a way that the line AB makes an angle less than 90° to the normal (dashed line EF in the top diagram above) at the surface of the glass prism (if the angle equals 90° refraction does not occur).
Line CD in the top diagram above represents the emergent ray, which in the experiment performed by students using a rectangular glass prism should be parallel to the incident ray. The line joining the intersections that the incident and emergent rays make with the opposite surfaces of the prism represent the refracted ray through the prism (line BC in the top diagram above).
Imagine a situation in which the two parallel lines representing the surfaces of the prism through which the incident and emergent rays intersect the opposite surfaces of the glass prism (PQ and RS in the top diagram above) are extended (dashed lines in the middle diagram above). Now move the prism so that it stays within these parallel lines in a direction opposite the path made by the rays indicating the direction of the incident, refracted and emergent rays (i.e., the prism is moved to the left in the middle diagram in the above).
As the point of intersection of the incident ray and the surface of the prism that it intersects moves closer to the corner Q, the refracted ray meets the corner R of the prism and, with further movement the refracted ray intersects the surface of the prism that is at right angles to the surface through which the incident ray enters the prism (point X in the lower diagram above). What then happens to the refracted ray? It can undergo one of two possibilities:
- further refraction through the surface of the prism at right angles to the surface through which the incident ray entered;
- reflection at the surface of the prism at right angles to the surface through which the incident ray entered.
Step 2: Range of Values That Can Be Taken by the Angles of Incidence and Refraction for a Glass Vs. a Water Prism
The above diagram shows an expanded and modified version of part of the lower diagram that was shown in the previous Step. The diagram is modified by showing:
- the normal drawn to the point of intersection of the refracted ray and the surface of a prism that is at right angles to the surface through which the incident ray entered the prism (dashed horizontal line).
- three angles, namely:
- i, the angle of incidence;
- r, the angle of refraction, which is also equal to the angle made by the refracted ray and the surface of a prism that is at right angles to the surface through which the incident ray entered the prism;
- (90 - r), the angle between the refracted ray and the normal drawn to the point of intersection of the refracted ray and the surface of a prism that is at right angles to the surface through which the incident ray entered the prism.
If a ray of light passes from air (refractive index taken as 1.00) into a material whose refractive index is n, then by Snell’s law:
sin i = n sin r
As i can take values between 0° and 90° (but not equal to these values), it follows from Snell’s law that r can take on values between 0° and arcsin (1/n) [arcsin (1/n) is the angle whose sine is equal to (1/n)].
Substituting values for i between 0° and 90° and for n in the equation for Snell’s law, one finds that:
- for glass of refractive index 1.5, r can vary between 0° and 41.81° and thus (90 - r) can vary between 48.19° and 90°;
- for water of refractive index 1.333, r can vary between 0° and 48.59° and thus (90 - r) can vary between 41.41° and 90°.
Step 3: Comparison of What Happens to a Refracted Ray That Hits the Surface of a Glass Vs. a Water Prism at Right Angles to the Surface Through Which the Incident Ray Enters
The upper values for the angles of refraction calculated in Step 2 (41.81° and 48.59° for glass and water, respectively) are also equal to the critical angles for glass and water, respectively.
As the range of values that (90 - r) can take for the rectangular glass prism is always greater than the critical angle for glass, the refracted ray is always reflected at the surface of the glass prism that is at right angles to the surface through which the incident ray entered the prism. Thus an emergent ray cannot emanate from the surface of the rectangular glass prism that is at right angles to the surface through which the incident ray entered the prism.
However, the range of values that (90 - r) can take for a water prism includes values less that the critical angle for water, and thus there is a range of values for r that allow the ray to be refracted through the surface of the rectangular water prism that is at right angles to the surface through which the incident ray entered the prism, namely, when r lies between 41.41° and 48.59° corresponding to values of i lying between 61.87° and 90°.
Step 4: Nature of the Emergent Ray for a Water Prism When Refraction Occurs at the Side of the Prism That Is at Right Angles to the Side of the Prism at Which the Incident Ray Entered
From the two equations:
sin i = n sin r
sin e = n sin (90 - r)
where e is the angle of emergence (the angle between the emergent ray and the normal to the surface of the water prism that the refracted ray hits after entering the water prism) it follows that:
sin e = (sin i) / (tan r)
Unlike the situation in the simple experiments performed by students where the incident ray and the emergent ray are parallel (e = i), this only happens with refraction occurring at the side of a water prism that is at right angles to the side of the prism at which the incident ray entered the prism when r = 45° (tan 45 = 1) and i = 70.53°.
In general, when refraction occurs at the side of a water prism that is at right angles to the side of the prism through which the incident ray entered, the incident and emergent rays are not parallel.
Step 5: A Justification of the Assumption That the Walls of a Thin-Walled Vessel Containing Water Do Not Significantly Alter the Path of Light Rays Passing Through the Water
The above diagram shows part of a transparent rectangular vessel containing water. The top and lower pairs of horizontal lines represent the parallel walls of a container with each wall having a thickness t. The middle pair of horizontal lines represents the water inside the container. The length from one inside wall to its opposite parallel wall is d.
A ray of light is shown leaving the outside of the container (composed of air) and entering the top wall of the vessel. This ray is refracted through the wall and its angle of incidence and angle of refraction is i and q respectively. The ray of light now passes from the wall into water. Relative to the wall-water interface its angle of incidence is q and its angle of refraction is r. The reverse process now occurs as the ray passes through the water to the opposite wall and then back to air.
The horizontal distance travelled by the ray as it enters the wall from the air and as it leaves the wall to enter the water is t tan q.
The horizontal distance travelled by the ray through the water layer is d tan r.
Thus the total horizontal distance travelled by the ray between entering and leaving the vessel is 2 t tan q + d tan r.
This expression can be simplified by noting that since the vessel wall has a higher refractive index than that of water, r is greater than q and that (d +2t) tan r is greater than 2 t tan q + d tan r.
Since the thickness of the wall of the vessel is much smaller than the width of water within the vessel (e.g., if t is 2 mm and d is 10 cm), d is much greater than t, tan r (d +2t) is approximately equal to d tan r.
If a water prism could maintain its shape without the presence of the container, d tan r would be the horizontal distance travelled by a refracted ray from one surface of the water prism to its opposite surface once a light ray entered a water prism.